Before we start ...
Just before we start I would like you to go through the concepts of General Tree (click here). In this way, you can get a quick brief about Trees in general and its keywords.
What problem does Binary Tree solve?
- In many different programming we have a thing called Sets. Sets are used to store multiple items in a single variable. Set is one of 4 built-in data types in Python used to store collections of data, the other 3 are List, Tuple, and Dictionary, all with different qualities and usage.
- Sets are more like Lists but there is a difference when we insert an element in a set it will make sure that those elements are unique to the set, unlike a list where duplicates can be present.
- Internally to implement set, one of the ways is using the Binary Search Tree.
What is Binary Tree?
- A binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.
- A Binary Search Tree it is a special case of Binary Tree where the elements have some kind of order in them. We can also say that it is an ordered or sorted Binary tree , is a rooted binary tree whose internal nodes each store a key greater than all the keys in the node's left subtree and less than those in its right subtree.
Searching in Binary Search Tree
- In the diagram below we can see that all the values less than the root node are placed on the left side of it and the greater ones are on the right side of the root node which is 15
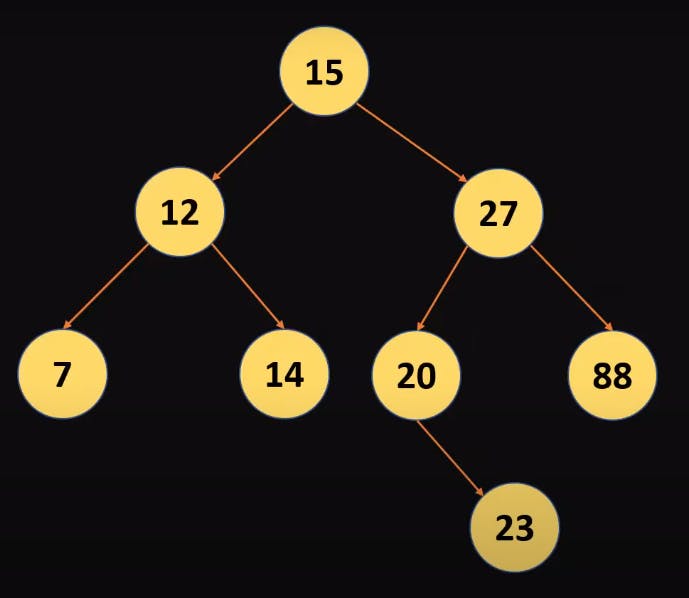
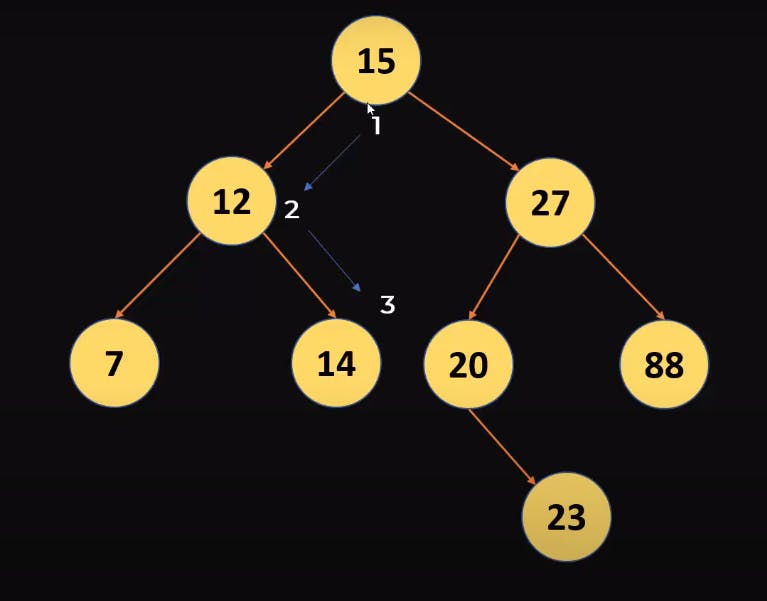
- Assume we want to search 14 in the above Binary Search Tree then first we will compare the root that is 15 so since 15 is greater than 14 so if 14 resides in the Tree hence it should be on the left side .
- When we search then we find 12 not 14 is greater than 12 hence it should be on the right side of the subtree.
- Below is a visual representation of how we just searched 14 in a binary search tree
Search Complexity
Since we reduced the space by 1/2 by every iteration.
- n = 8
- 8->4->2->1
- if there are 8 elements hence we got 3 iteration
- log8 = 3
- Search Complexity = O(log n)
Inserting in Binary Search Tree
- Let's assume we want to insert and element 13 in the same binary search tree.
- We will first compare it with 15 since 13 is less than 15 hence it will go to the left side of the root 15 node.
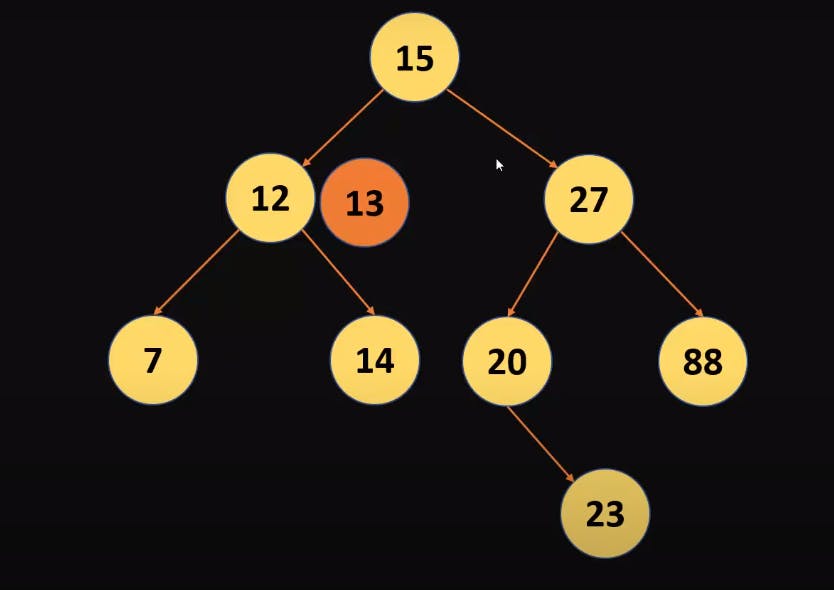
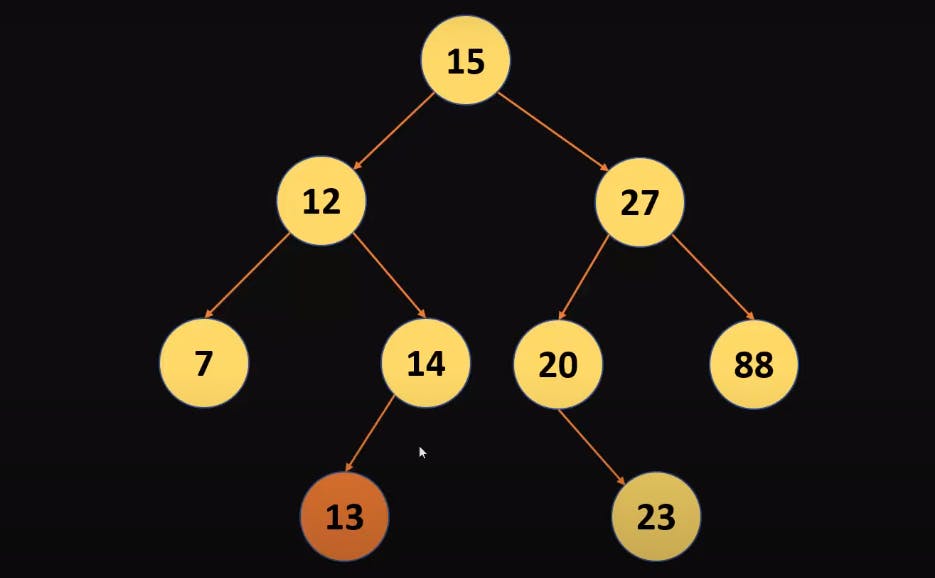
- Now you realize that 13 is greater than the current 12 hence it will go to the right subtree of 12.
- We have 14 here and 13 is less than 14 hence it will go to the left subtree of 14.
Breadth First Search (BFS) and Depth First Search(DFS)
- Any process for visiting all of the nodes in some order is called a traversal. There are two technique for this: BFS and DFS
BFS
- BFS stands for Breadth-First Search is a vertex-based technique for finding the shortest path in the graph. It uses a Queue data structure which follows first in first out. In BFS, one vertex is selected at a time when it is visited and marked then its adjacent are visited and stored in the queue. It is slower than DFS if we take the below example.
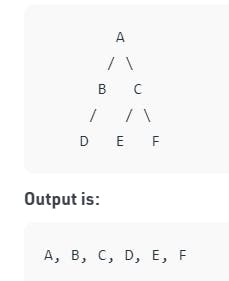
DFS
- DFS stands for Depth First Search is an edge-based technique. It uses the Stack data structure, performs two stages, first visited vertices are pushed into the stack and second if there are no vertices then visited vertices are popped.
There are three types of traversals in DFS -
- In-order Traversal : Traverse the left subtree -> Visit the root -> Traverse the right subtree.
- Pre-order Traversal : Visit the root ->Traverse the left subtree ->Traverse the right subtree
- Post-order Traversal : Traverse the left subtree -> Traverse the right subtree -> Visit the root.
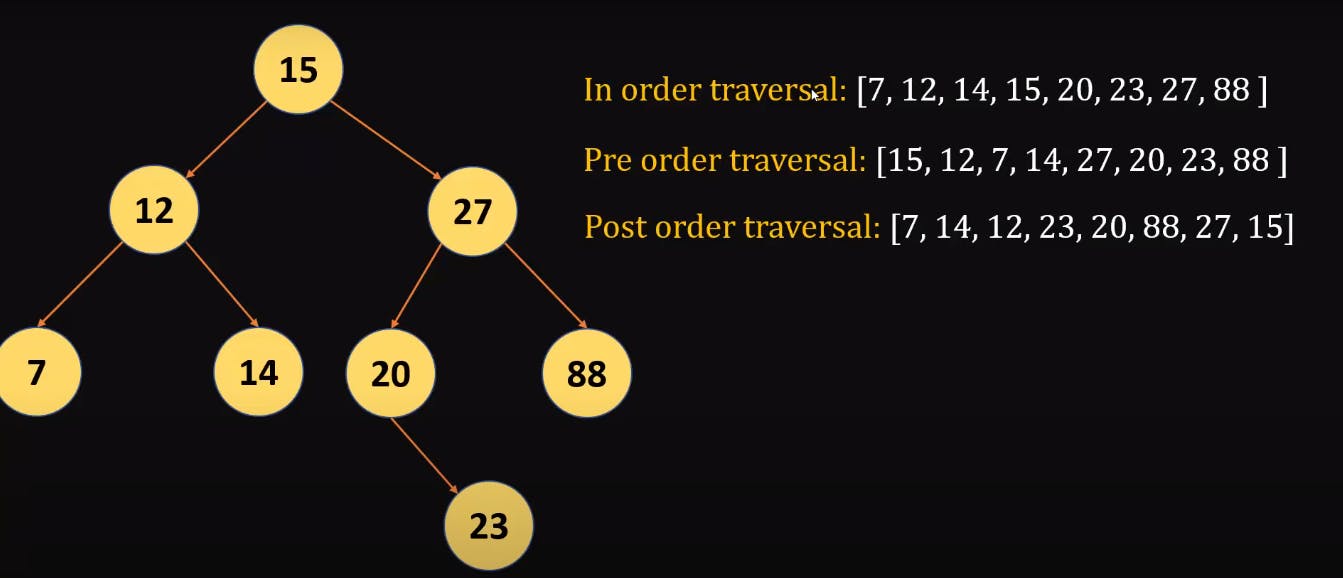
Let's Implement In-order Traversal using Python
- Creating a base class with a init function.
class BinarySearchTreeNode:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
- Adding an Add child function to the base class.
def add_child(self,data):
if data == self.data:
return
if data<self.data:
#add data in the left sub tree
if self.left:
self.left.add_child(data)
else:
self.left = BinarySearchTreeNode(data)
else:
if self.right:
self.right.add_child(data)
else:
self.right = BinarySearchTreeNode(data)
#add data in the right sub tree
- Creating a function for In order Traversal
def in_order_traversal(self):
elements = []
if self.left:
elements += self.left.in_order_traversal()
#visiting the left tree
#now add the root or the base node to the element list
elements.append(self.data)
#now we need to visit the right sub tree
if self.right:
elements += self.right.in_order_traversal()
return elements
- defining a search operation
def search(self,value):
if self.data == value:
return True
if value < self.data:
#then the value might be in the left subtree
if self.left:#to check if we have a left subtree
return self.left.search(value)
else:
return False
if value > self.data:
#then the value might be in the right subtree
if self.right:#to check if we have a right subtree
return self.right.search(value)
else:
return False
- Finally, we will define a Help function for creating Initializing the class
def build_tree(element):
root = BinarySearchTreeNode(element[0])
for i in range(1,len(element)):
root.add_child(element[i])
return root
- Yes we are almost done , Let's Put all the code together into a single program.
class BinarySearchTreeNode:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
def add_child(self,data):
if data == self.data:
return
if data<self.data:
#add data in the left sub tree
if self.left:
self.left.add_child(data)
else:
self.left = BinarySearchTreeNode(data)
else:
if self.right:
self.right.add_child(data)
else:
self.right = BinarySearchTreeNode(data)
#add data in the right sub tree
def in_order_traversal(self):
elements = []
if self.left:
elements += self.left.in_order_traversal()
#visiting the left tree
#now add the root or the base node to the element list
elements.append(self.data)
#now we need to visit the right sub tree
if self.right:
elements += self.right.in_order_traversal()
return elements
def search(self,value):
if self.data == value:
return True
if value < self.data:
#then the value might be in the left subtree
if self.left:#to check if we have a left subtree
return self.left.search(value)
else:
return False
if value > self.data:
#then the value might be in the right subtree
if self.right:#to check if we have a right subtree
return self.right.search(value)
else:
return False
def build_tree(element):
root = BinarySearchTreeNode(element[0])
for i in range(1,len(element)):
root.add_child(element[i])
return root
if __name__ == '__main__':
numbers = [3,4,6,7,32,5,6,7,54,34,56]
newtree = build_tree(numbers)
print(newtree.in_order_traversal())
print(newtree.search(20))
- The output of the code will be -
[3, 4, 5, 6, 7, 32, 34, 54, 56]
False
Let's revise the properties of a Binary Search Tree
- All the elements should be unique to the Tree
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
Node Deletion in a Binary
There are 3 scenarios which we can face while deleting a Node in a binary search tree. Lets look on those -
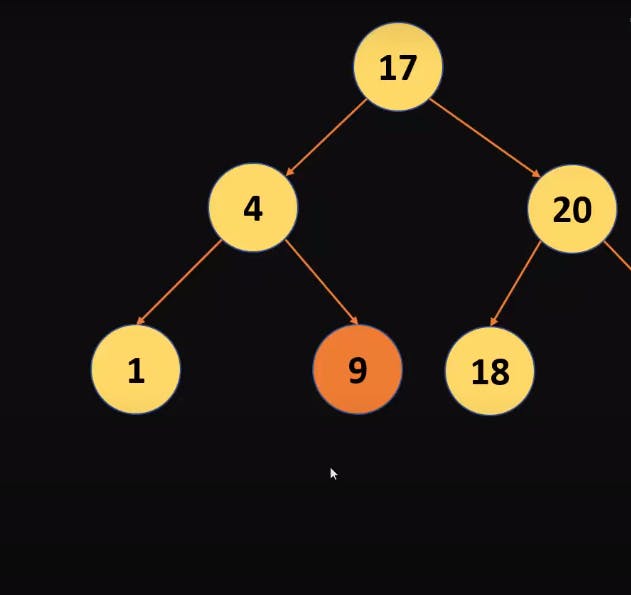
Deleting a node with no child
Let's Take the example of the below Tree. You want to delete 9 which doesn't have any child node . This is very simple because we can directly delete the node without rearranging the Tree.
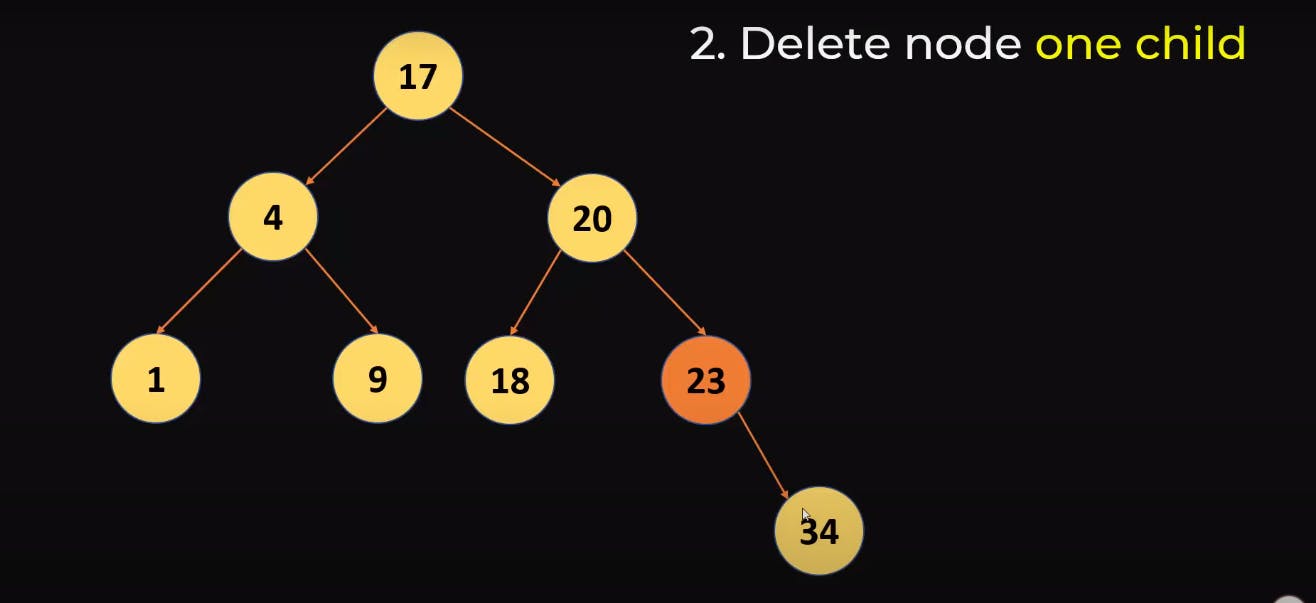
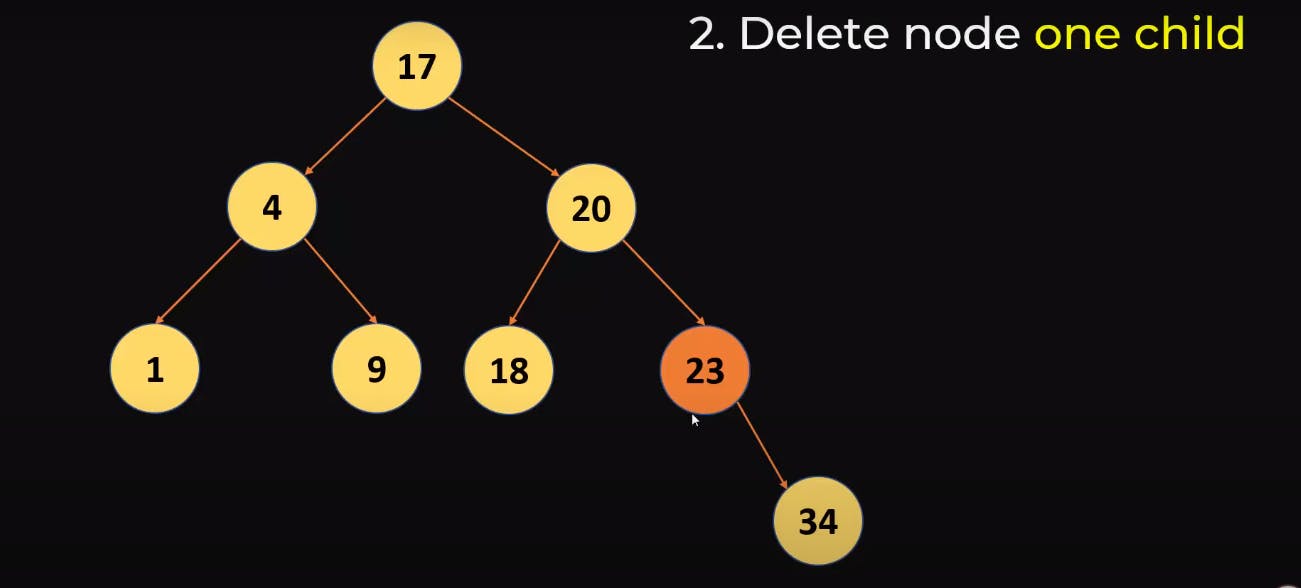
Deleting a node with one child
This is also simple, just we need to replace the child with the deleted node , as we can see in the below example we need to delete 23 so we will just replace it with 34
Deleting a node with two child
This one is a bit tricky because we need to delete the node and also maintain the property of Binary search tree. In the below example we are deleting 20, which has 2 child nodes
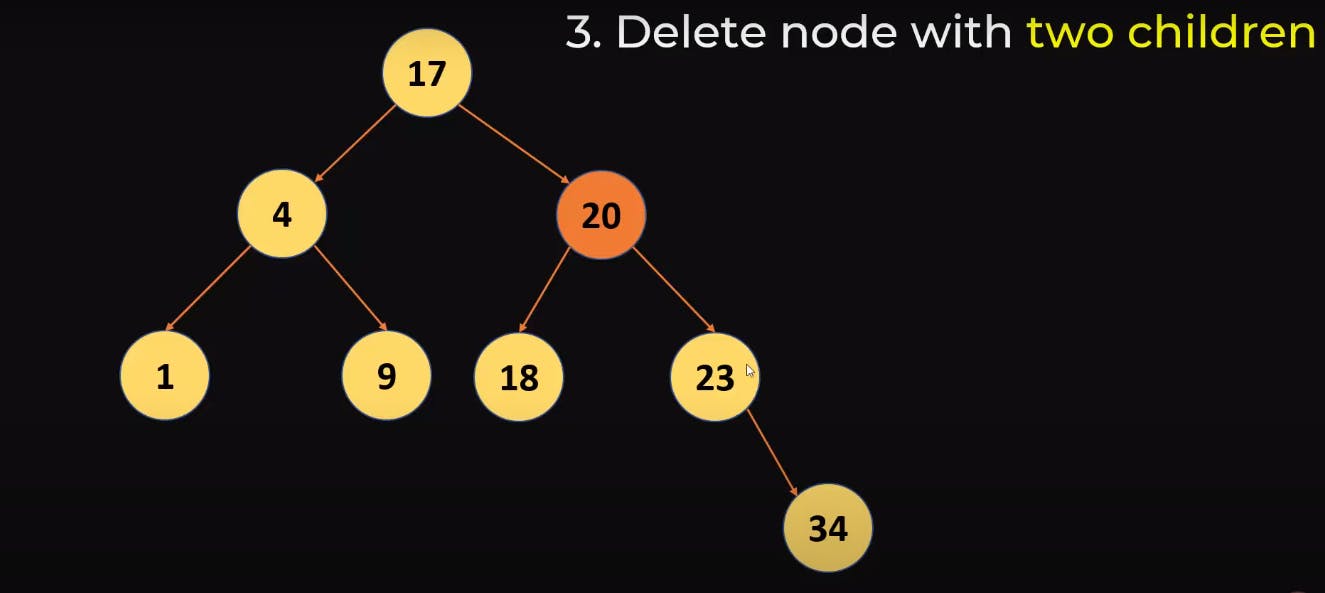
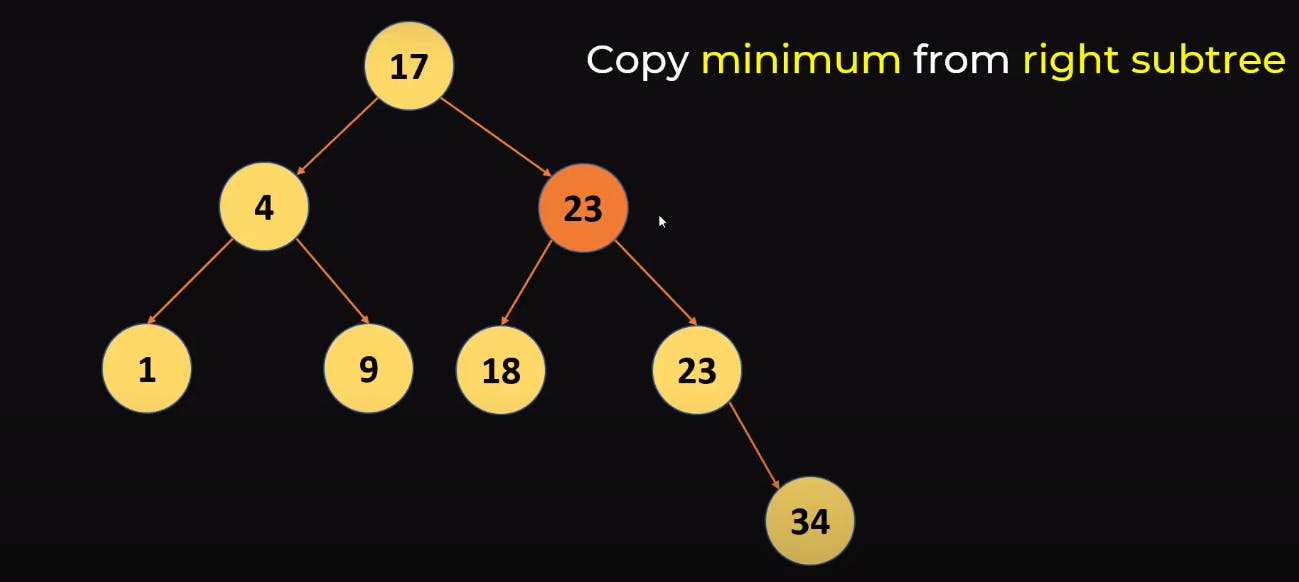
The steps to do this is:
- Copy the minimum value from the right subtree, hence all the values which are right will remain greater and then
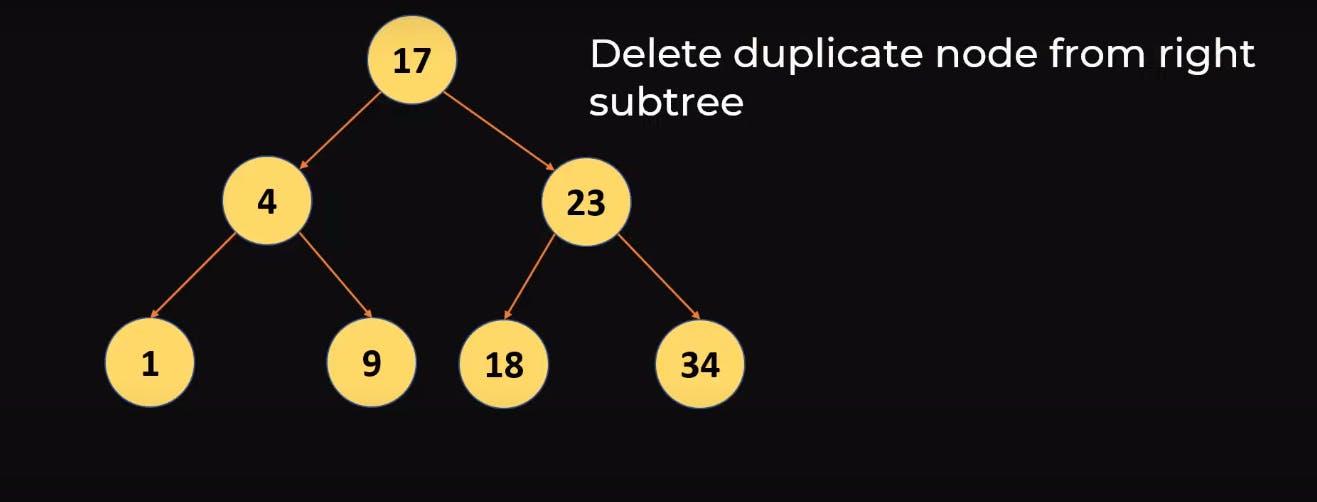
- Delete the duplicate from the right subtree
Alternate approach:
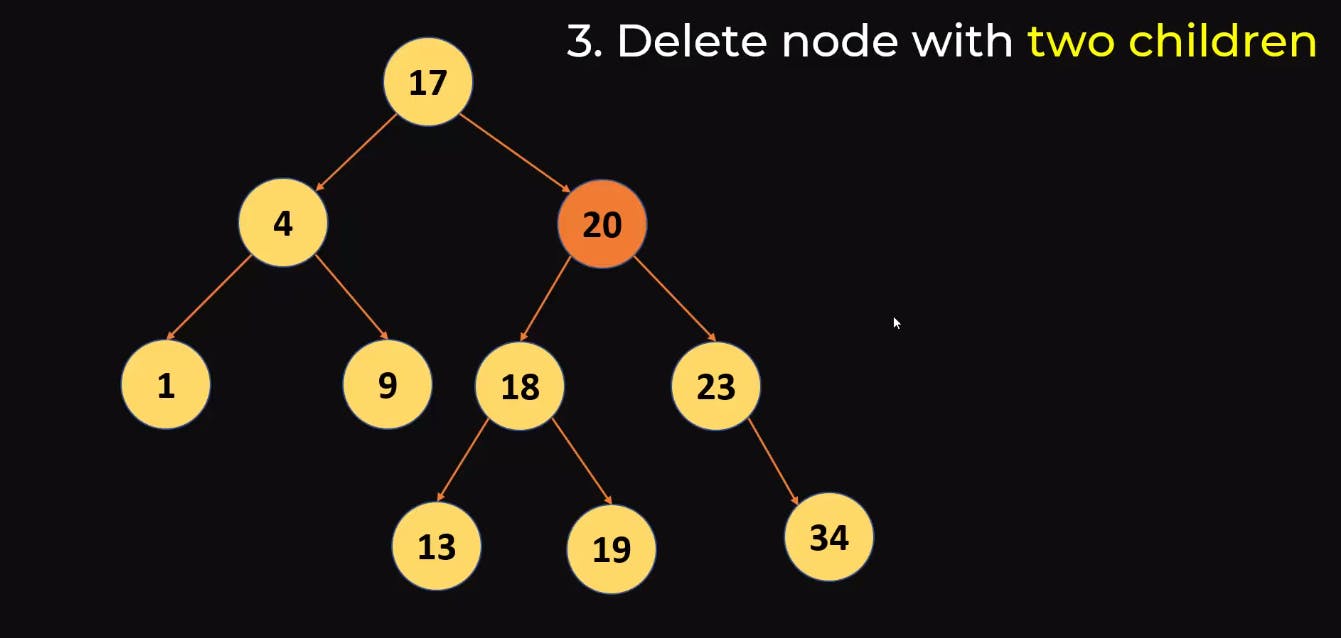
- You can also look into left Sub Tree and find the maximum from there.
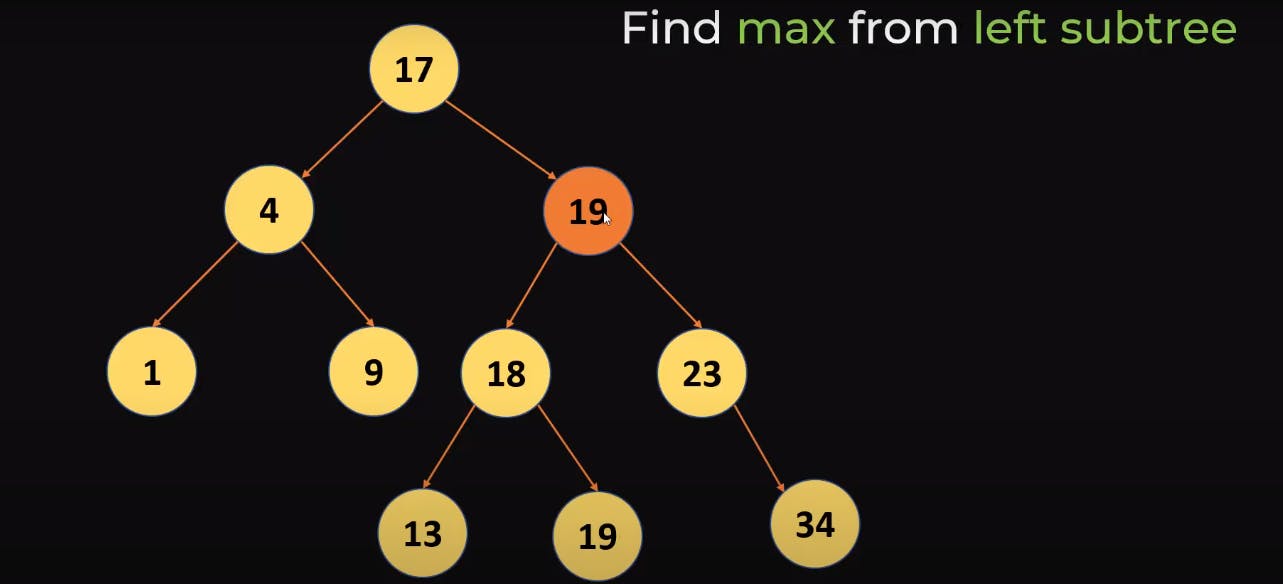
- copy that maximum value and then we can delete the copy, as we did below, we replaced 20 with the maximum value in the left subtree which is 19 and then deleted the copy of 19.
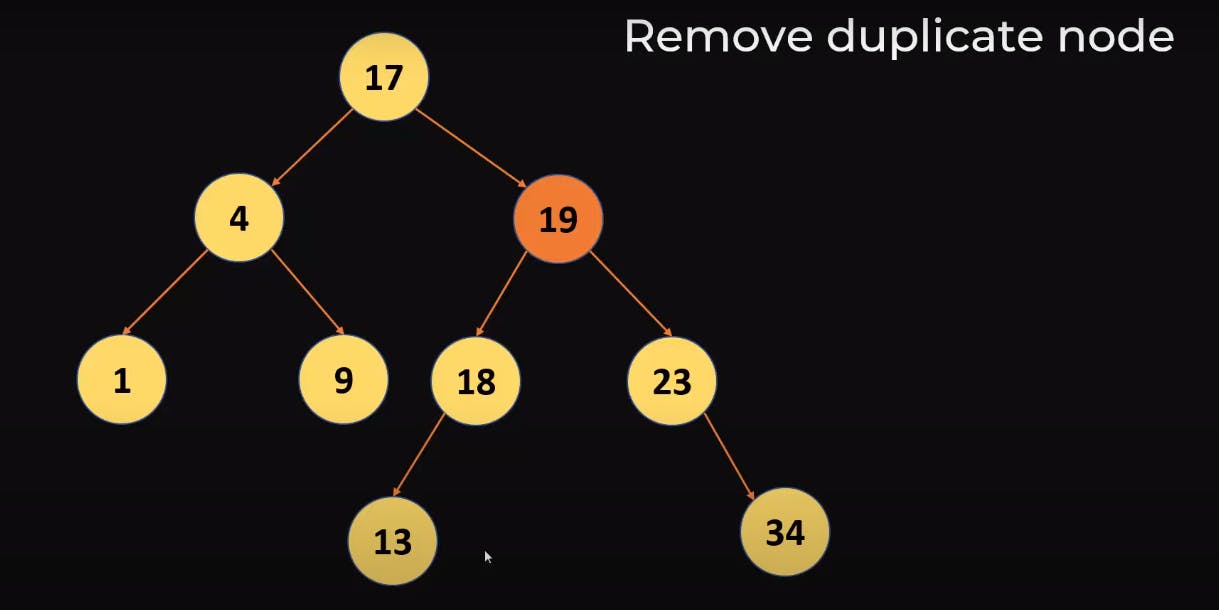
Let's Implement Deletion of a Node using Python
- So we will use the Above Tree class which we created during the Traversal.
class BinarySearchTreeNode:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
def add_child(self,data):
if data == self.data:
return
if data<self.data:
#add data in the left sub tree
if self.left:
self.left.add_child(data)
else:
self.left = BinarySearchTreeNode(data)
else:
if self.right:
self.right.add_child(data)
else:
self.right = BinarySearchTreeNode(data)
#add data in the right sub tree
def in_order_traversal(self):
elements = []
if self.left:
elements += self.left.in_order_traversal()
#visiting the left tree
#now add the root or the base node to the element list
elements.append(self.data)
#now we need to visit the right sub tree
if self.right:
elements += self.right.in_order_traversal()
return elements
- Now let us create a function for finding the maximum value in the tree, which we might use in the deletion later.
def find_max(self):
if self.right:
return self.right.find_max()
return self.data
- Similarly, we will create a function for finding the minimum value in the tree, which we will use in the deletion later.
def find_min(self):
if self.left:
return self.left.find_max()
return self.data
- Finally, let's add the Delete function which will take care of all the circumstances which occurs during the Deletion of a particular Node.
def delete(self,value):
if value < self.data:
if self.left:
self.left = self.left.delete(value)
elif value > self.data:
if self.right:
self.right = self.right.delete(value)
else:
if self.left is None and self.right is None :
return None
elif self.left is None:
return self.right
elif self.right is None:
return self.left
min_value = self.right.find_min()
self.data = min_value
self.right = self.right.delete(min_value)
return self
- We need a Helper function for creating the Tree Node and building it.
def build_tree(element):
root = BinarySearchTreeNode(element[0])
for i in range(1,len(element)):
root.add_child(element[i])
return root
- Let's us Now implement all these functions in a single program and merge it with the Original Binary Tree Class.
class BinarySearchTreeNode:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
def add_child(self,data):
if data == self.data:
return
if data<self.data:
#add data in the left sub tree
if self.left:
self.left.add_child(data)
else:
self.left = BinarySearchTreeNode(data)
else:
if self.right:
self.right.add_child(data)
else:
self.right = BinarySearchTreeNode(data)
#add data in the right sub tree
def in_order_traversal(self):
elements = []
if self.left:
elements += self.left.in_order_traversal()
#visiting the left tree
#now add the root or the base node to the element list
elements.append(self.data)
#now we need to visit the right sub tree
if self.right:
elements += self.right.in_order_traversal()
return elements
def search(self,value):
if self.data == value:
return True
if value < self.data:
#then the value might be in the left subtree
if self.left:#to check if we have a left subtree
return self.left.search(value)
else:
return False
if value > self.data:
#then the value might be in the right subtree
if self.right:#to check if we have a right subtree
return self.right.search(value)
else:
return False
def find_max(self):
if self.right:
return self.right.find_max()
return self.data
def find_min(self):
if self.left:
return self.left.find_max()
return self.data
def delete(self,value):
if value < self.data:
if self.left:
self.left = self.left.delete(value)
elif value > self.data:
if self.right:
self.right = self.right.delete(value)
else:
if self.left is None and self.right is None :
return None
elif self.left is None:
return self.right
elif self.right is None:
return self.left
min_value = self.right.find_min()
self.data = min_value
self.right = self.right.delete(min_value)
return self
def build_tree(element):
root = BinarySearchTreeNode(element[0])
for i in range(1,len(element)):
root.add_child(element[i])
return root
if __name__ == '__main__':
numbers = [3,4,6,7,32,5,6,7,54,34,56]
newtree = build_tree(numbers)
print(newtree.in_order_traversal())
#print(newtree.search(20))
#print(f'{newtree.find_max()} is the maximum')
#print(f'{newtree.find_min()} is the minimum')
newtree.delete(4)
print(newtree.in_order_traversal())
- The element will be deleted.
Thank-you!
I am glad you made it to the end of this article. I hope you got to learn something, if so please leave a Like which will encourage me for my upcoming write-ups.
- My GitHub Repos
- Connect with me on Linkedin
- Start your own blogs

